如何用计算器算年金现值等

如何用计算器算年金现值等

增长型年金的计算方式不建议用计算器计算，用计算器计算出来的数字不如公式来的准确。

 期末增长型年金现值=PV(n,(r-g)/(1+g),C,BGN)(1+r)，即以C为PMT,以（r-g）/(1+g)为折现率的期初年金，再除以1+r，用r*=(1+r)/(1+g)-1算出来的也只是估计值。

年金现值计算公式：

P=[1-(1+i)的-n次方]/i，P是年金现值因子，设普通年金1元、利率为i、n期的年金现值，记作（P/A，i，n）。

年金是指等额、定期的系列支出。例如，分期付款赊购、分期偿还贷款等。

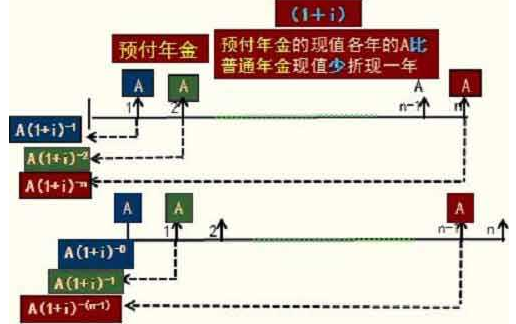
年金有普通年金、预付年金、递延年金和永续年金。

普通年金又称后付年金，是指各期期末收付的年金。普通年金现值，是指为在每期期末取得相等金额的款项，现在需要投入的金额。

扩展资料：

如果年金的期数很多，用上述方法计算终值显然相当繁琐。由于每年支付额相等，折算终值的系数又是有规律的，所以，可找出简便的计算方法。

设每年的支付金额为A，利率为i，期数为n，则按复利计算的年金终值S为：

S=A×(1+i）^0+…+A×(1+i)^(n-1)，(1)

等式两边同乘以(1+i)：

S(1+i)=A(1+i)^1+…+A(1+l)^(n)，（n等均为次方）（2)

上式两边相减可得：

S(1+i)-S=A(1+i)^n-A,

S=A[（1+i）^n-1]/i

式中[（1+i）n-1]/i的为普通年金、利率为i，经过n期的年金终值记作(S/A，i,n),可查普通年金终值系数表。

参考资料来源：百度百科-年金现值系数