如图在Rt三角形ABC中

如图在Rt三角形ABC中

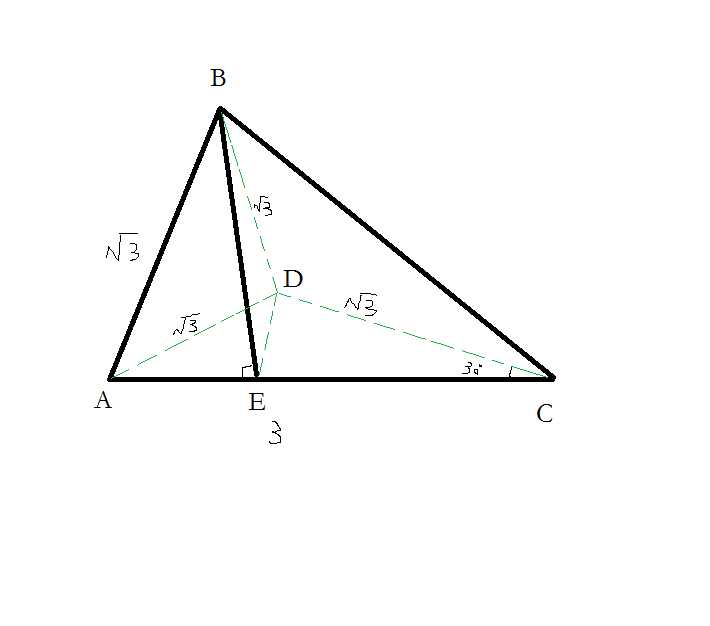
（1）证明：∵点E是点B在平面ADC上的射影，

           ∴BE⊥平面ADE，ED、AE分别为BD、BA在平面ADE内的射影

           ∵BD=AB

           ∴AE=DE，

           ∴∠DAE=∠ADE=30度，

           在△ADC中，AC=3，AD=CD=√3

           由余弦定理得∠ADC=120度，

          ∴∠CDE=90º，即CD⊥DE，

          又BE⊥平面ADE，即BE⊥CD，

          ∴CD⊥平面BDE

（2）如图

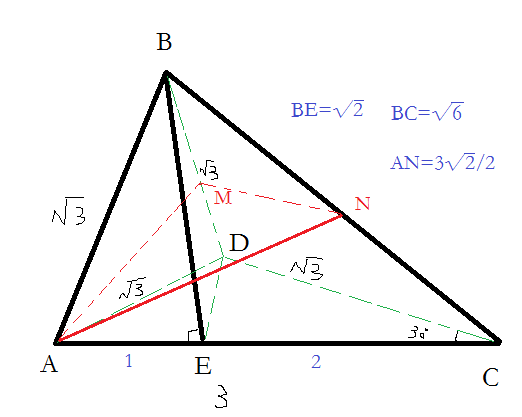
取BD得中点M，过点M做MN∥CD，连接AM,AN

∵△ABD是等边三角形，CD⊥面BDE

∴AM⊥BD,MN⊥BD

∴∠AMN是面A-BD-C的二面角

在等腰三角形ADE中，AD=√3，∠DAE=∠ADE=30º,AE=DE

∴AE=DE=1,EC=2

∵△ABE是直角三角形，AB是斜边，∠AEB=90º

∴BE=√2

∴BC=√6

∴BN=√6/2

在△ABC中，AB^2+BC^2=3+6=9，AC^2=9

∴AB^2+BC^2=AC^2

∴△ABC是直角三角形，∠ABC=90º

∴AN=√AB^2+BN^2=3√2/2

又在△AMN中，AM=3/2，MN=√3/2

∴cos∠AMN=(AM^2+MN^2-AN^2)/(2AM*MN)=-√3/3