五边形如何一条线分成两个三角形

五边形如何一条线分成两个三角形

根据数学上“线”的概念，线是无宽度的长度，那么就可以用一条足够粗的线，线的宽度和五边形的一边长度相同，用这条粗线从五边形中和它宽度相同的边垂直划过，那么这剩余的四边和那一条粗线所组成的便就是两个三角形了。如下图：

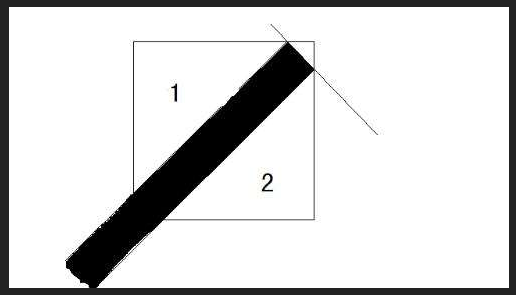
线是由无数个点集合成的图形，线的性质有：

1、一线的两端是点。

2、直线是它上面的点一样地平放着的线。

3、过两点有作且有一条直线。

4、线段(有限直线)可以无限地延长。

5、同平面内一条直线和另外两条直线相交，若在直线同侧的两个内角之和小于180°，则这两条直线经无限延长后在这一侧一定相交。

扩展资料

完美五边形

德国数学家卡尔·莱因哈特于1918年发现了五种可以镶嵌平面的五边形，从那时起，寻找可以镶嵌平面的五边形并将它们分类就成为了一个数学世纪难题。

很多人都认为莱因哈特已经把所有可以镶嵌平面的五边形都找出来了，但事实并非如此：1968年，R·B·克什纳又发现了三种；1975年，理查德·詹姆斯将纪录刷新到了9种。

1985年，罗尔夫·施泰因发现了第14种。似乎这样的五边形还会越来越多。不过，在那之后五边形追踪行动似乎陷入了低谷。

2015年8月19日，美国华盛顿大学研究团队发现了一种新的不规则五边形，相互组合后可完全铺满平面，不会出现重迭或有任何空隙，是全球第15种能做到此效果的五边形。