复合函数的概念是什么?
的有关信息介绍如下:要理解复合函数,先要知道基本初等函数的概念:
一般来讲,基本初等函数归为以下五类:
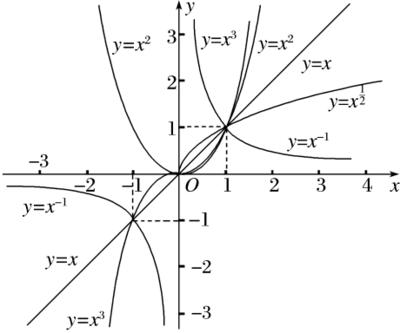
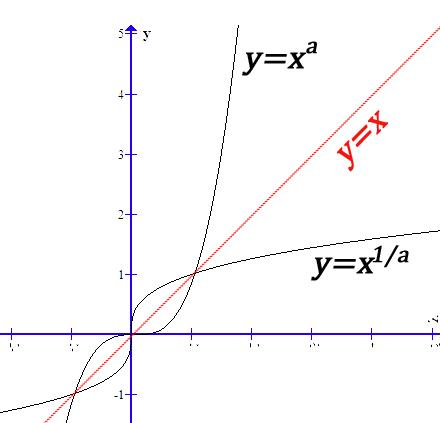
幂函数:f(x)=xᵃ(a为有理数);
指数函数:f(x)=aˣ(a>0且a≠1);
对数函数:f(x)=logₐ(x)(a>0且a≠1);
三角函数:f(x)=sin(x)、f(x)=cos(x)...
反三角函数:f(x)=arcsin(x)、f(x)=arccos(x)...
复合函数通俗地说就是函数套函数,是把上述几种基本初等函数的函数复合为一个较为复杂的函数。复合函数中含有两个及以上的函数,如y=sin(u),u=2ᵛ,v=x²,则函数y=sin[2^(x²)]就是y关于x的复合函数,其中x是自变量,u、v都是中间变量,y是应变量。
不是任何两个函数放在一起都能构成一个复合函数,复合的过程中要掌握一个原则:内层函数的值域要在其外层函数的定义域内,由内到外,逐层满足,如y=log₂[1-cos(x)]没问题,但y=log₂[cos(x)-2]就不行,显然没有任何x能使y有意义,故求复合函数的定义域时,要综合考虑各部分的x的取值范围,最后取他们的交集,还是以y=log₂[1-cos(x)]为例:内层cos(x):定义域x∈R;外层log₂[u]:u>0→1-cos(x)>0→函数的定义域x≠2kπ。
复合函数的性质:
周期性:复合函数的最小正周期为内外层函数最小正周期的最小公倍数,如tan[sin(x)]的最小正周期为2π
单调(增减)性
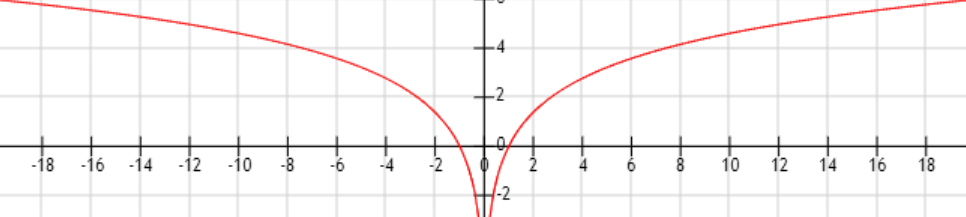
依内外层的单调性来决定:即“增+增=增;减+减=增;增+减=减;减+增=减”,可以简化为口诀“同增异减”。如y=ln(x²):
外层为增函数,内层x<0时为减函数,x>0时为增函数,故复合后:
x<0时,内外层增减性相异→复合后为减函数;
x>0时,内外层增减性相同→复合后为增函数;