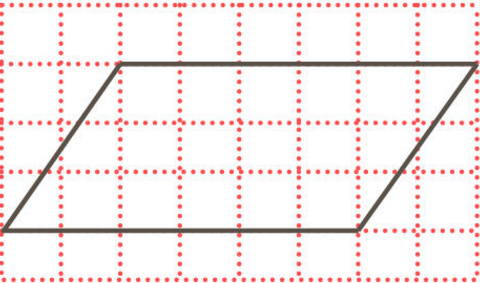
在平行四边形ABCD中
的有关信息介绍如下:
(1) ∠A=∠DBC又 ∠C=∠A故△BCD为等腰三角形,BD=CD=10△ABD为等腰三角形,AB=BD=10sinA=sinC=4/5, cosA=3/5∠ABD=180-2*Asin∠ABD=sin(180-2*A)=sin2*A=2sinA*cosA=24/25由正弦定理AD=BD*sin∠ABD/sinA=10*(24/25)/(4/5)=12∠BEF=∠DBC=∠BDE∠EBF=∠DBE∴△BDE∽△BEFBE/BD=BF/BEBE/10=y/BEBE^2=10y又cos∠BDE=cosC=3/5由余弦定理cos∠BDE=(DE^2+BD^2-BE^2)/2DE*BD,即[(12-x)^2+10^2-10y]/2(12-x)*10=3/5,化简得y=(x^2-12x+100)/100版权声明:文章由 去问问 整理收集,来源于互联网或者用户投稿,如有侵权,请联系我们,我们会立即处理。如转载请保留本文链接:https://www.qwenw.com/article/408426.html