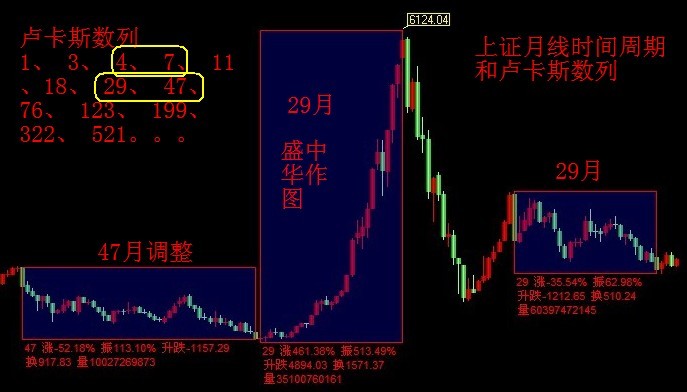
卢卡斯数列的基本概述

卢卡斯数列的基本概述

卢卡斯数列的通项公式为 f(n)=[(1+√5）/2]^n+[(1-√5)/2]^n

先定义整数 P 和 Q ，使满足一元二次方程判断法则： △ = P^2 - 4Q > 0，

从而得一方程 x^2 - Px + Q = 0，其根为 a, b。

现定义卢卡斯数列为：

Un(P,Q) = (a^n - b^n) / (a-b) 及 Vn(P,Q) = a^n + b^n

其中 n 为非负整数，得 U0(P,Q) = 0、 U1(P,Q) = 1 、 V0(P,Q) = 2 、 V1(P,Q) = P、......

我们有下列和卢卡斯数列相关的恒等式：

Um+n = UmVn - a^nb^nUm-n 、 Vm+n = VmVn - a^nb^nVm-n

Um+1 = P*Um - Q*Um-1 、 Vm+1 = P*Vm - Q*Vm-1 (取 n = 1)

U2n = UnVn 、 V2n = Vn2 - 2*Qn

U2n+1 = Un+1Vn - Qn 、 V2n+1 = Vn+1Vn - PQn

若取 (P,Q) = (1,-1)，我们便有 Un 为斐波那契数，

即 0、 1、 1、 2、 3、 5、 8、 13、 21、 34、 55、 89、 144、 233、 377、 610、 987、 1597、 2584、 4181、 6765等。

而 Vn 为卢卡斯数 (Lucas Number)，

即 2、 1、 3、 4、 7、 11、18、 29、 47、 76、 123、 199、 322、 521、 843、 1364、 2207、 3571、 5778、 9349 等。

若取 (P,Q) = (2,-1)，我们便有 Un 为佩尔数 (Pell Number)，

即 0、 1、 2、 5、 12、 29、 70、 169、 408、 985、 2378、 5741等。

而 Vn 为佩尔 - 卢卡斯数 (Pell - Lucas Number) (详见另文《佩尔数列》)，

即 2、 2、 6、 14、 34、 82、 198、 478、 1154、 2786、 6726等。

此等全都是数学界很有名的数列。