循环冗余校验码怎么算？

循环冗余校验码怎么算？

循环冗余校验码的计算方法：

编码原理：

现假设有：有效信息：M；

除数G（生成多项式）有：M/G=Q+R/G；

此时，可选择R作为校验位，则MR即为校验码。

校验原理：（M-R）/G=Q+0/G

说明：以接收到的校验码除以约定的除数，若余数为0，则可认为接收到的数据是正确的。

例：有效信息1101，生成多项式样1011

循环校验码解：

有效信息1101(k=4)，即M(x)=x3+x2+x0，生成多项式1011(r+1=4,即r=3)；

即G(x)=x3+x1+x0，M(x)·x3=x6+x5+x3，即1101000（对1101左移三位）；

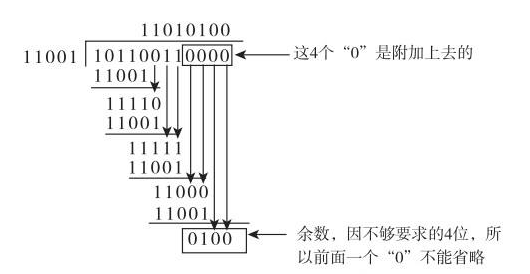
M(x)·x3/G(x)=1101000/1011=1111+001/1011    即1010的CRC是：1101001 。

计算图文如下 ：

CRC（Cyclic Redundancy Check）循环冗余校验码，是常用的校验码，在早期的通信中运用广泛，因为早期的通信技术不够可靠（不可靠性的来源是通信技术决定的，比如电磁波通信时受雷电等因素的影响），不可靠的通信就会带来‘确认信息’的困惑，书上提到红军和蓝军通信联合进攻山下的敌军的例子，第一天红军发了条信息要蓝军第二天一起进攻，蓝军收到之后，发一条确认信息，但是蓝军担心的是‘确认信息’如果也不可靠而没有成功到达红军那里，那自己不是很危险？于是红军再发一条‘对确认的确认信息’，但同样的问题还是不能解决，红军仍然不敢贸然行动。