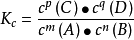方程 D=(B-A)/B(W-A) , B-A在分子 ,B*(W-A)在分母。如何对A求偏导?(对A求偏导,B,W均可认为是常数
的有关信息介绍如下:
先调整一下方程,D = 1/B * [B/(W-A) - A/(W-A)] = 1/B * [B/(W-A) - (A-W)/(W-A) - W/(W-A)] = 1/B * [B/(W-A) + 1 -W/(W-A)] 再对变量D对于A偏导,1/B是常数,1对于A求偏导是0, 于是3项变2项,1/B * B/(W-A) = 1/(W-A) = - 1/(A-W), 其偏导是1/(W-A)^2(因为(x-c)^-1的导数是-(x-c)^2= -(c-x)^2),剩下的1项是-1/B*W/(W-A) = 1/B*W/(A-W),1/B*W是常数,于是其导数是-1/B*W/(W-A)^2,于是D的导数是1/(W-A)^2 -1/B*W/(W-A)^2 = (B-W)/B(W-A)^2。此即是我们想要的结果。 可清楚了?
版权声明:文章由 去问问 整理收集,来源于互联网或者用户投稿,如有侵权,请联系我们,我们会立即处理。如转载请保留本文链接:https://www.qwenw.com/life/384148.html