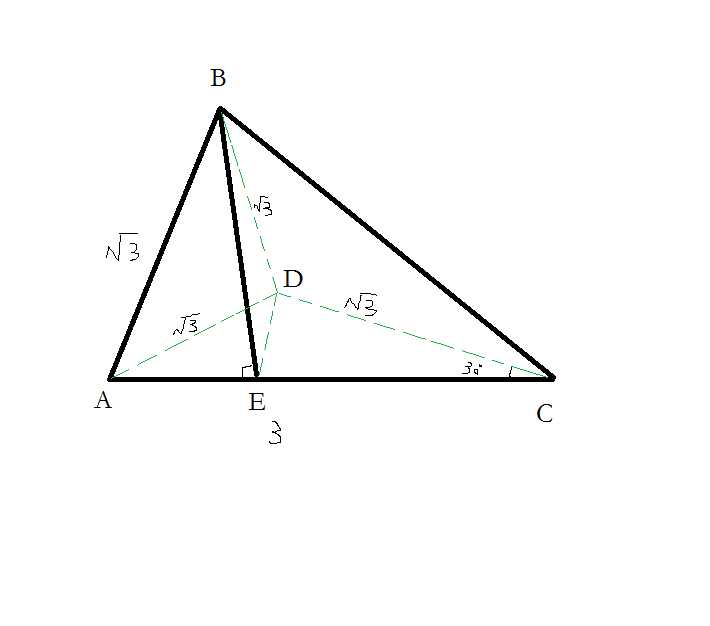
求三角形边长公式

求三角形边长公式

三角形边长公式：

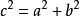
公式描述：公式中a，b分别为直角三角形两直角边，c为斜边。

斜边上的高是两条直角边在斜边的射影的比例中项，每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项。是数学图形计算的重要定理。

三角形中，如果有一个锐角等于30°，那么它所对的直角边等于斜边的一半。三角形中，如果有一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°。

证明方法：

如图，Rt△ABC中，∠BAC=90°，AD是斜边BC上的高，则有射影定理如下：

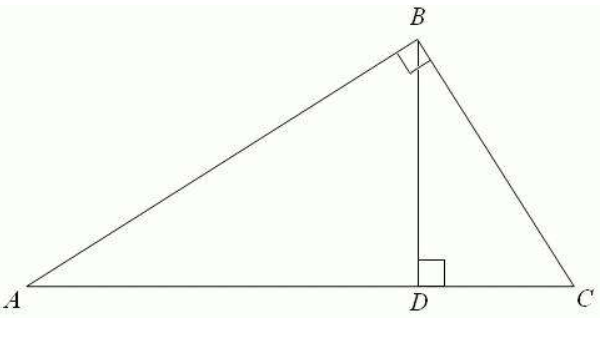
（1）（AD)²=BD·DC。

（2）（AB)²=BD·BC。

（3）（AC)²=CD·BC。

性质：

1 、在平面上三角形的内角和等于180°。

2 、在平面上三角形的外角和等于360°。

3、 在平面上三角形的外角等于与其不相邻的两个内角之和。

4、 一个三角形的三个内角中最少有两个锐角。

5、 在三角形中至少有一个角大于等于60度，也至少有一个角小于等于60度。

6 、三角形任意两边之和大于第三边，任意两边之差小于第三边。

7、 在一个直角三角形中，若一个角等于30度，则30度角所对的直角边是斜边的一半。

8、直角三角形的两条直角边的平方和等于斜边的平方。

9、直角三角形斜边的中线等于斜边的一半。