求转速，角速度，之间的关系

求转速，角速度，之间的关系

转速与角速度换算关系：ω=2πn。

转速n：是指单位时间内，物体做圆周运动的次数，用符号"n"表示；其国际标准单位为r/S （转/秒）

角速度ω：一个以弧度为单位的圆(一个圆周为2π,即:360度=2π),在单位时间内所走的弧度即为角速度。公式为:ω=φ/t(Ч为所走过弧度，t为时间)ω的单位为：弧度每秒 。

扩展资料：

角速度的特性

1、伪矢量性：角速度是在物理学中描述物体转动时在单位时间内转过角度以及转动方向的矢量（更准确地说，是伪矢量）。

2、角速度的矢量性：v=ω×r，其中，×表示矢量相乘(叉乘)，方向由右手螺旋定则确定，r为矢径，方向由圆心向外。

三维坐标系下的角速度

在三维坐标系中，角速度变得比较复杂。在此状况下，角速度通常被当作向量来看待；甚至更精确一点要当作伪向量。它不只具有数值，而且同时具有方向的特性。数值指的是单位时间内的角度变化率，而方向则是用来描述转动轴的。概念上，可以利用右手定则来标示角速度伪向量的正方向。

二维坐标系下的角速度

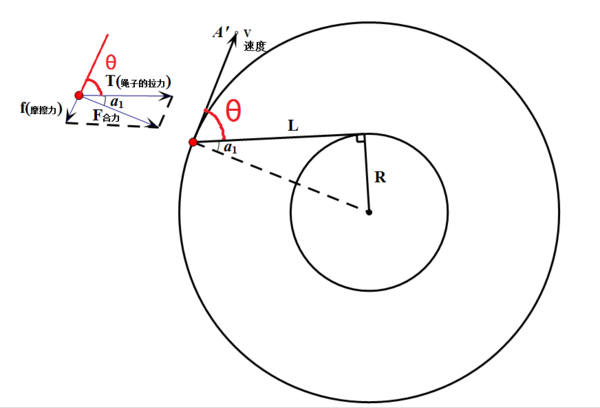
一个质点在二维平面上的角速度是最容易懂的。 如右图所示，假使从(O)点向(P)质点画一条直线，则该粒子的速度向量()可分成在沿着径向上分量(径向分量)以及垂直于径向的分量(切线方向分量)。

参考资料来源：百度百科-角速度